Statsmodels库的学习历程:回归分析
1.问题引入
粮食产量的影响因素有很多,现从粮食作物播种面积、有效灌溉面积、农用化肥施用折纯量、农业机械总动力、农村用电量、成灾面积这6个因素着手分析,具体数据如下所示:
年份 粮食产量(万吨) 粮食作物播种面积(千公顷) 有效灌溉面积(千公顷) 农用化肥施用折纯量(万吨) 农业机械总动力(万千瓦) 农村用电量(亿千瓦小时) 成灾面积(千公顷)
1991 43529.3 112313.6 47822.07 2805.1 29388.6 963.2 27810
1992 44265.8 110559.7 48590.1 2930.2 30308.4 1107.1 25900
1993 45648.8 110508.7 48727.9 3151.9 31816.6 1244.9 23130
1994 44510.1 109543.7 48759.1 3317.9 33802.5 1473.9 31380
1995 46661.8 110060.4 49281.2 3593.7 36118.05 1655.66 22270
1996 50453.5 112547.92 50381.4 3827.93 38546.92 1812.7 21230
1997 49417.1 112912.1 51238.5 3980.7 42015.64 1980.1 30310
1998 51229.53 113787.4 52295.6 4085.6 45207.71 2042.1 25180
1999 50838.58 113160.98 53158.41 4124.32 48996.12 2173.4 26730
2000 46217.52 108462.54 53820.33 4146.41 52573.61 2421.3 34370
2001 45263.67 106080.04 54249.39 4253.76 55172.1 2610.8 31790
2002 45705.75 103890.83 54354.85 4339.39 57929.85 2993.4 27160
2003 43069.53 99410.37 54014.23 4411.56 60386.54 3432.9 32520
2004 46946.95 101606.03 54478.42 4636.58 64027.91 3933 16300
2005 48402.19 104278.38 55029.34 4766.22 68397.85 4375.7 19970
2006 49804.23 104957.7 55750.5 4927.69 72522.12 4895.82 24630
2007 50413.85 105998.62 56518.34 5107.83 76589.56 5509.93 25060
2008 53434.29 107544.51 58471.68 5239.02 82190.41 5713.15 22280
2009 53940.86 110255.09 59261.45 5404.35 87496.1 6104.44 21230
2010 55911.31 111695.42 60347.7 5561.68 92780.48 6632.35 18540
2011 58849.33 112980.35 61681.56 5704.24 97734.66 7139.62 12440
2012 61222.62 114368.04 62490.52 5838.85 102558.96 7508.46 11470
2013 63048.2 115907.54 63473.3 5911.86 103906.75 8549.52 14300
2014 63964.83 117455.18 64539.53 5995.94 108056.58 8884.45 12680
2015 66060.27 118962.81 65872.64 6022.6 111728.07 9026.92 12380
2016 66043.51 119230.06 67140.62 5984.41 97245.59 9238.26 13670
2017 66160.73 117989.06 67815.57 5859.41 98783.35 9524.42 9200
2018 65789.22 117038.21 68271.64 5653.42 100371.74 9358.54 10569
2019 66384.34 116063.6 68678.61 5403.59 102758.26 9482.87 7913
2020 66949.15 116768.17 69160.52 5250.65 105622.15 6210.98 7993
2021 68284.75 117630.82 69609.48 5191.26 107764.32 6736.3 4682
2022 68652.77 118332.11 70358.87 5079.2 110597.19 7765.57 4373
2023 69540.99 118968.54 71644 5021.74 113742.57 7991.9 4797
数据下载地址:
https://data.stats.gov.cn/easyquery.htm?cn=C01
2.多元线性回归分析
2.1.多元线性回归模型构建
采取最小二乘法对数据进行多元线性回归,输出结果如下所示:
OLS Regression Results
==============================================================================
Dep. Variable: 粮食产量(万吨) R-squared: 0.994
Model: OLS Adj. R-squared: 0.993
Method: Least Squares F-statistic: 759.9
Date: Wed, 25 Jun 2025 Prob (F-statistic): 6.51e-28
Time: 00:58:55 Log-Likelihood: -262.04
No. Observations: 33 AIC: 538.1
Df Residuals: 26 BIC: 548.6
Df Model: 6
Covariance Type: nonrobust
=================================================================================
coef std err t P>|t| [0.025 0.975]
---------------------------------------------------------------------------------
const -4.792e+04 5953.134 -8.050 0.000 -6.02e+04 -3.57e+04
粮食作物播种面积(千公顷) 0.5598 0.040 14.154 0.000 0.479 0.641
有效灌溉面积(千公顷) 0.6415 0.090 7.164 0.000 0.457 0.826
农用化肥施用折纯量(万吨) 1.9010 0.605 3.144 0.004 0.658 3.144
农业机械总动力(万千瓦) -0.0155 0.031 -0.507 0.616 -0.078 0.047
农村用电量(亿千瓦小时) -0.2667 0.205 -1.300 0.205 -0.689 0.155
成灾面积(千公顷) -0.1999 0.036 -5.491 0.000 -0.275 -0.125
==============================================================================
Omnibus: 3.104 Durbin-Watson: 1.199
Prob(Omnibus): 0.212 Jarque-Bera (JB): 1.440
Skew: -0.040 Prob(JB): 0.487
Kurtosis: 1.980 Cond. No. 6.67e+06
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 6.67e+06. This might indicate that there are
strong multicollinearity or other numerical problems.
从上面的运行结果可以看出,方程的拟合优度R2=0.994,调整后的拟合优度为0.993,说明模型拟合效果很好。F值(F=759.9)较大,且P值(P=6.51e-28)<0.01,表明方程从整体上有较好的解释能力。但是在5%的显著水平下,农业机械总动力(t检验的P值为0.616,大于0.05的显著性水平)、农村用电量(t检验的P值为0.205,大于0.05的显著性水平)均没有通过t检验,另外粮食总产量与农业机械总动力、农村用电量均成负相关,这与经济意义上的是有矛盾的,说明变量之间可能存在多重共线性,这可能会导致回归模型的不稳定性和不准确性。(虽然成灾面积也与粮食产量成负相关,但是符合经济学意义的)
2.2.多重共线性检验与处理
绘制各变量之间的相关性热力图,输出结果如下所示:
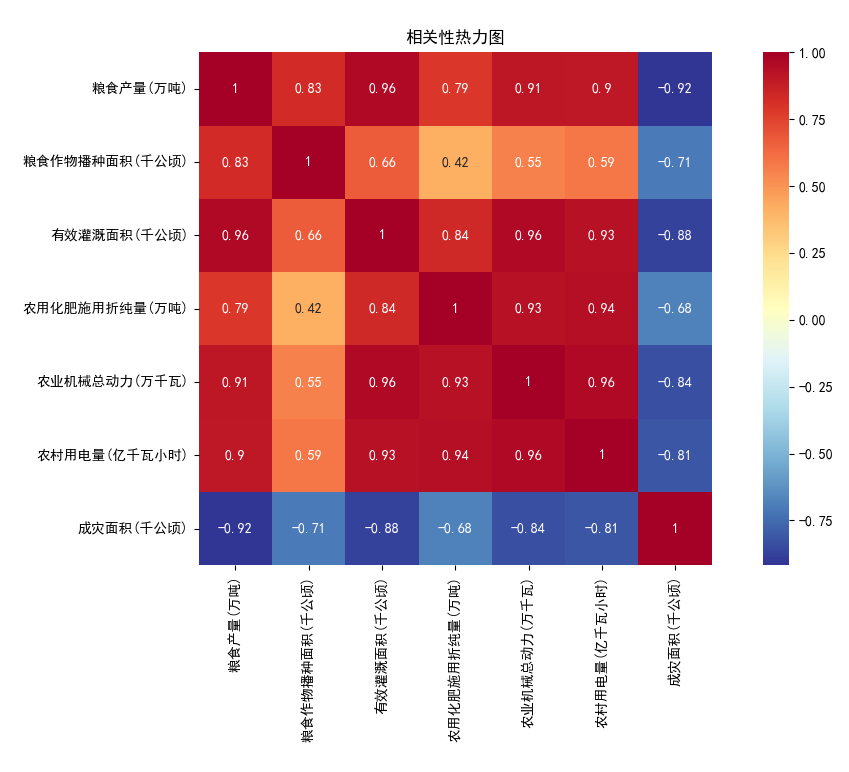
由上图可知,在这6个因素中,只有成灾面积与粮食产量成负相关性,是符合经济学意义的,而农业机械总动力、农村用电量这2个因素与粮食产量成正相关性,与前文多元线性回归结果相悖,各自变量之间的相关性比较强(相关性在0.7以上),可以初步判断自变量之间存在多重共线性。
通过计算方差膨胀因子(VIF)来检测各自变量的相关性程度,一般地,如果VIF>10(为何是10?VIF的计算公式为:$VIF=\frac{1}{1-R^2}$,一般地,当拟合优度$R^2>0.9$时,我们认为模型的结果是可接受的,说明自变量与因变量之间存在较强的相关关系,但是,在这里,我们计算VIF值时,不是以粮食产量为因变量,而是让各自变量轮流做因变量,剩余自变量继续做自变量,继续进行多元回归来研究自变量之间的相关关系,因此,在自变量之间构建的多元回归模型中,拟合优度越高的,反而会导致多重共线性问题的出现,需要对其因变量进行剔除处理。严格的话,以VIF>5为基准),则认为自变量之间存在严重的多重共线性,各自变量的VIF计算结果如下所示:
feature VIF
0 const 1994.126433
1 粮食作物播种面积(千公顷) 2.508362
2 有效灌溉面积(千公顷) 25.228616
3 农用化肥施用折纯量(万吨) 18.034679
4 农业机械总动力(万千瓦) 43.246328
5 农村用电量(亿千瓦小时) 20.297767
6 成灾面积(千公顷) 5.745064
采取逐步回归法,对VIF值大于5的自变量进行剔除处理,重新计算VIF值,计算结果如下所示:
feature VIF
0 const 1171.598154
1 粮食作物播种面积(千公顷) 2.014224
2 农用化肥施用折纯量(万吨) 1.877755
3 成灾面积(千公顷) 3.076186
由上述结果可知,当剔除有效灌溉面积、农业机械总动力、农村用电量后,所有自变量的VIF值都在5以下,可以重新进行多元回归模型的构建。(常数项const只参与计算,其VIF值不用于比较大小)
多元线性回归模型输出结果如下所示:
OLS Regression Results
==============================================================================
Dep. Variable: 粮食产量(万吨) R-squared: 0.969
Model: OLS Adj. R-squared: 0.965
Method: Least Squares F-statistic: 299.1
Date: Wed, 25 Jun 2025 Prob (F-statistic): 6.68e-22
Time: 00:58:55 Log-Likelihood: -290.24
No. Observations: 33 AIC: 588.5
Df Residuals: 29 BIC: 594.5
Df Model: 3
Covariance Type: nonrobust
=================================================================================
coef std err t P>|t| [0.025 0.975]
---------------------------------------------------------------------------------
const -2.769e+04 1.02e+04 -2.728 0.011 -4.85e+04 -6929.618
粮食作物播种面积(千公顷) 0.6693 0.079 8.488 0.000 0.508 0.831
农用化肥施用折纯量(万吨) 3.3238 0.434 7.656 0.000 2.436 4.212
成灾面积(千公顷) -0.4159 0.059 -7.018 0.000 -0.537 -0.295
==============================================================================
Omnibus: 3.632 Durbin-Watson: 0.945
Prob(Omnibus): 0.163 Jarque-Bera (JB): 1.655
Skew: 0.166 Prob(JB): 0.437
Kurtosis: 1.954 Cond. No. 3.89e+06
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 3.89e+06. This might indicate that there are
strong multicollinearity or other numerical problems.
从上面的运行结果可以看出,方程的拟合优度R2=0.969,调整后的拟合优度为0.965,说明模型拟合效果很好。F值(F=299.1)较大,且P值(P=6.68e-22)<0.01,表明方程从整体上有较好的解释能力。另外的,各自变量均通过了显著性水平为5%的t检验,说明每个自变量均对因变量存在独立的显著影响,其作用并非随机误差导致,模型设定较为合理。
2.3.残差的正态性检验
绘制残差直方图和Q-Q图,输出结果如下所示:
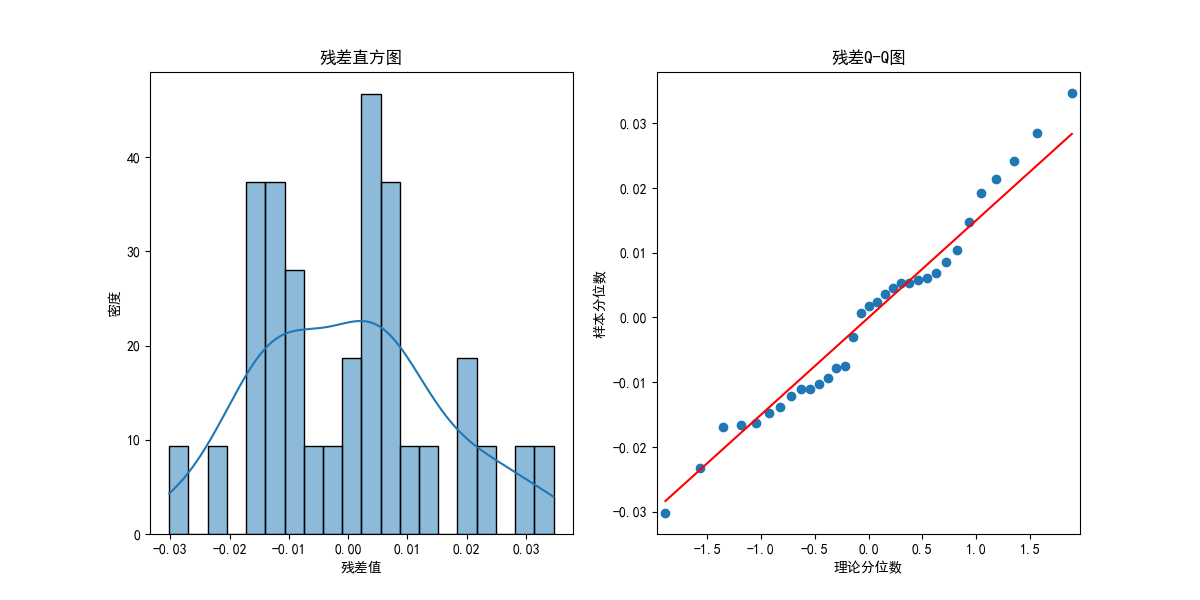
对于残差直方图,主要观察分布是否接近钟形曲线,由图可知,残差直方图基本上呈现单峰对称分布,峰值居中(均值接近0),大体上服从正态分布;从残差Q-Q图来看,散点紧密贴合对角线(红色参考线),可以初步判断残差服从正态分布。
计算残差均值和标准差,以及进行Shapiro-Wilk检验,输出结果如下所示:
残差均值: 7.077522406523877e-11
残差标准差: 1597.3424442253965
Shapiro-Wilk检验统计量: 0.9623495936393738
Shapiro-Wilk检验p值: 0.30079397559165955
从上述结果来看,残差均值接近0(科学计数法表示约等于0),表明模型整体无系统性偏差,正负残差基本平衡;残差标准差绝对值较大,说明数据离散程度较高,但由于粮食产量这一因变量本身数值比较大,也是合理的;在Shapiro-Wilk检验中,统计量为0.96,越接近1表明数据越符合正态分布;p值为0.30,大于0.05显著性水平,不能拒绝残差服从正态分布的原假设,即残差服从正态分布。残差均值为0且服从正态分布,说明线性模型假设成立。
2.4.残差的自相关性检验
绘制残差滞后图,输出结果如下所示:
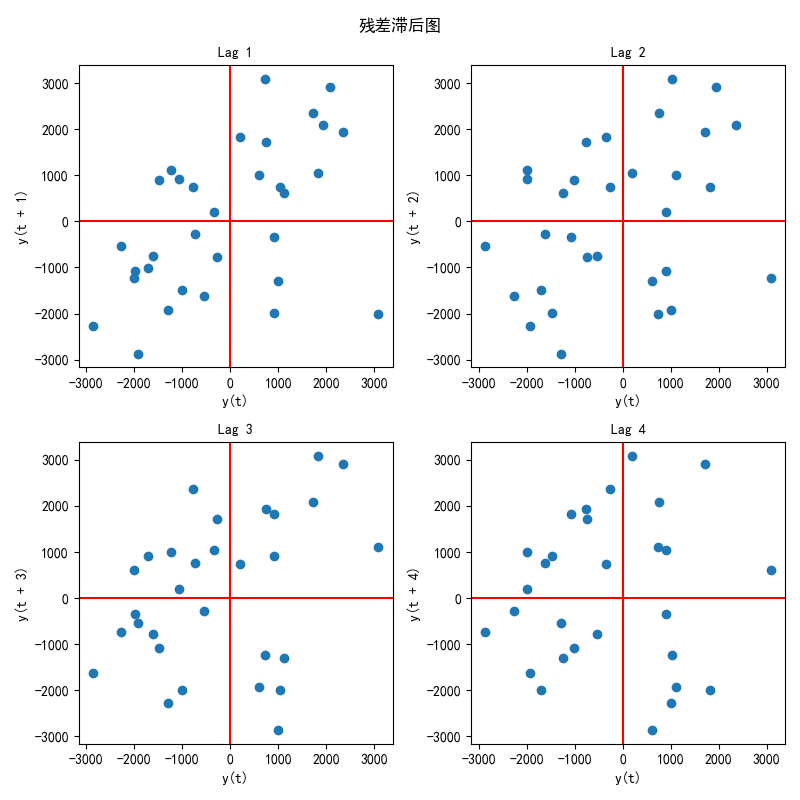
如果散点主要分布在第一和第三象限且呈现递增趋势,就认为存在正相关性;如果散点主要分布在第二和第四象限且呈现递减趋势,就认为存在负相关性。由上述结果初步认为,残差没有明显的自相关性。为了进一步验证此结论,继续进行Durbin-Watson检验,输出结果如下所示:
DW值:0.9449340892338773
ρ值:0.5275329553830613
通过对比以下表格,可以判断残差是否存在自相关性。
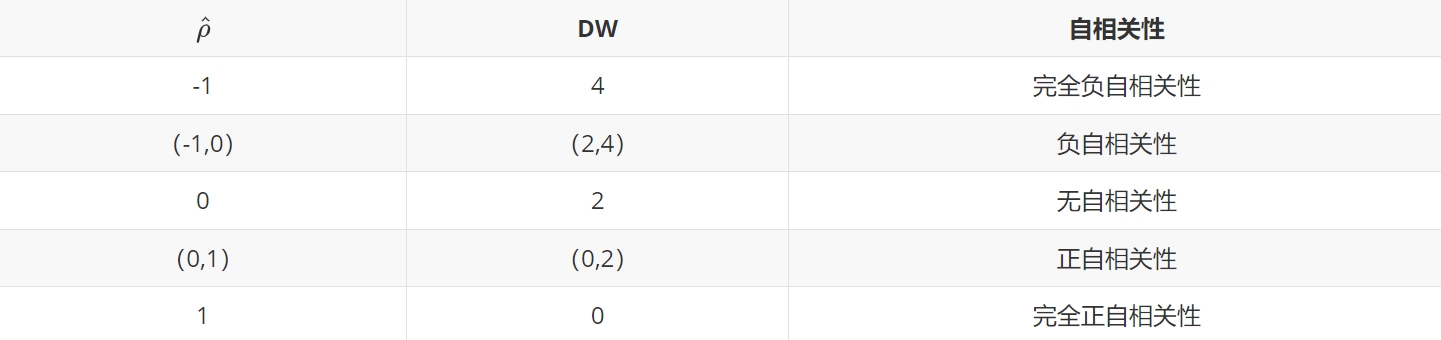
也可以表述为:
- 检验统计量DW越接近0,就越有证据表明正序列相关。
- 检验统计量DW为2,表示不存在序列相关性。
- 检验统计量DW越接近4,就越有证据表明负序列相关。
一般地,检验统计值DW在1.5到2.5之间被认为是正常的,即不存在序列相关性,但是,前面求得DW值为0.94,超出此范围,表明残差存在序列自相关性,并不是前文初步判断的那样没有明显的自相关性,现通过取对数的方式来消除残差自相关性的影响,输出结果如下所示:
OLS Regression Results
==============================================================================
Dep. Variable: 粮食产量(万吨) R-squared: 0.991
Model: OLS Adj. R-squared: 0.991
Method: Least Squares F-statistic: 1125.
Date: Wed, 25 Jun 2025 Prob (F-statistic): 4.30e-30
Time: 00:58:55 Log-Likelihood: 91.758
No. Observations: 33 AIC: -175.5
Df Residuals: 29 BIC: -169.5
Df Model: 3
Covariance Type: nonrobust
=================================================================================
coef std err t P>|t| [0.025 0.975]
---------------------------------------------------------------------------------
const -6.6550 0.997 -6.675 0.000 -8.694 -4.616
粮食作物播种面积(千公顷) 1.3626 0.080 17.091 0.000 1.200 1.526
农用化肥施用折纯量(万吨) 0.3229 0.016 20.214 0.000 0.290 0.356
成灾面积(千公顷) -0.1038 0.008 -13.664 0.000 -0.119 -0.088
==============================================================================
Omnibus: 0.715 Durbin-Watson: 1.517
Prob(Omnibus): 0.700 Jarque-Bera (JB): 0.741
Skew: 0.311 Prob(JB): 0.690
Kurtosis: 2.610 Cond. No. 6.24e+03
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 6.24e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
从上述结果可知,Durbin-Watson值为1.517,趋近于2,说明不存在系列自相关性,通过了残差自相关性检验。
2.5.异方差检验
常用的异方差检验方法有White检验、BP检验等,在这里,使用White检验进行求解,输出结果如下所示:
White检验统计量: 12.634428518202728
White检验p值: 0.1798575333199947
由上述结果可知,White检验的p值为0.18,大于0.05的显著性水平,无法拒绝不存在异方差的原假设,即多元回归模型无异方差,通过了异方差检验。
2.6.多元线性回归模型的确定
虽然不存在异方差,但为了能获得更精确的参数估计和更窄的置信区间,现在使用“最小二乘法+稳健标准误”继续完善多元线性回归模型的构建,输出结果如下所示:
OLS Regression Results
==============================================================================
Dep. Variable: 粮食产量(万吨) R-squared: 0.991
Model: OLS Adj. R-squared: 0.991
Method: Least Squares F-statistic: 1236.
Date: Wed, 25 Jun 2025 Prob (F-statistic): 1.11e-30
Time: 00:58:55 Log-Likelihood: 91.758
No. Observations: 33 AIC: -175.5
Df Residuals: 29 BIC: -169.5
Df Model: 3
Covariance Type: HC3
=================================================================================
coef std err z P>|z| [0.025 0.975]
---------------------------------------------------------------------------------
const -6.6550 0.951 -7.001 0.000 -8.518 -4.792
粮食作物播种面积(千公顷) 1.3626 0.078 17.378 0.000 1.209 1.516
农用化肥施用折纯量(万吨) 0.3229 0.014 23.878 0.000 0.296 0.349
成灾面积(千公顷) -0.1038 0.007 -15.453 0.000 -0.117 -0.091
==============================================================================
Omnibus: 0.715 Durbin-Watson: 1.517
Prob(Omnibus): 0.700 Jarque-Bera (JB): 0.741
Skew: 0.311 Prob(JB): 0.690
Kurtosis: 2.610 Cond. No. 6.24e+03
==============================================================================
Notes:
[1] Standard Errors are heteroscedasticity robust (HC3)
[2] The condition number is large, 6.24e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
由上述结果可知,多元线性回归方程可表示为:

3.python程序
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import MinMaxScaler
from statsmodels.stats.outliers_influence import variance_inflation_factor
from scipy.stats import shapiro
from pandas.plotting import lag_plot
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
data = pd.read_excel(io='数据.xlsx', index_col=0)
X = data.iloc[:, 1:]
y = data.iloc[:, 0]
X = sm.add_constant(X)
model = sm.OLS(y, X)
result = model.fit()
print('多元线性回归模型的初步构建:\n', result.summary())
data_std = pd.DataFrame(MinMaxScaler().fit_transform(data))
pearson = data_std.corr(method='pearson')
sns.heatmap(pearson, square=True, annot=True, cmap='RdYlBu_r', xticklabels=data.columns, yticklabels=data.columns)
plt.title('相关性热力图')
plt.subplots_adjust(left=0.2, right=0.8, top=0.85, bottom=0.25)
# 多重共线性检验
VIF = [variance_inflation_factor(X, i) for i in range(X.shape[1])]
VIF = pd.DataFrame({'feature': X.columns, 'VIF': VIF})
print('\n多重共线性检验:\n', VIF)
def process(X, col):
X = X.loc[:, col]
VIF = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])][1:]
if max(VIF) >= 5:
index = np.argmax(VIF) + 1
del col[index]
return process(X, col)
else:
VIF = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
VIF = pd.DataFrame({'feature': col, 'VIF': VIF})
return VIF
VIF = process(X, X.columns.tolist())
print('\n逐步回归法剔除高相关变量后再次进行多重共线性检验:\n', VIF)
model = sm.OLS(y, X[VIF['feature'].values])
result = model.fit()
print('\n剔除高相关变量后的多元线性回归模型的构建:\n', result.summary())
# 残差正态性检验
residuals = result.resid
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
sns.histplot(residuals, kde=True, stat='density', bins=20)
plt.title('残差直方图')
plt.xlabel('残差值')
plt.ylabel('密度')
plt.subplot(1, 2, 2)
sm.qqplot(residuals, line='s', ax=plt.gca())
plt.title('残差Q-Q图')
plt.xlabel('理论分位数')
plt.ylabel('样本分位数')
mean_residuals = np.mean(residuals)
std_residuals = np.std(residuals)
print('\n残差正态性检验:\n残差均值:', mean_residuals)
print('残差标准差:', std_residuals)
stat, p_value = shapiro(residuals)
print('Shapiro-Wilk检验统计量:', stat)
print('Shapiro-Wilk检验p值:', p_value)
# 残差自相关性检验
plt.figure(figsize=(8, 8))
for i in range(4):
plt.subplot(2, 2, i + 1)
lag_plot(pd.Series(residuals), lag=i + 1)
plt.title(f'Lag {i + 1}', fontsize=10)
plt.axhline(y=0, color='r', linestyle='-')
plt.axvline(x=0, color='r', linestyle='-')
plt.suptitle('残差滞后图')
plt.tight_layout()
DW = sm.stats.durbin_watson(residuals)
rho = 1 - 0.5 * DW
print(f'\n残差自相关性检验:\nDW值:{DW}\nρ值:{rho}')
X = X[VIF['feature'].values]
data_yX = pd.concat([y, X], axis=1)
data_yX = np.log(data_yX)
data_yX['const'] = 1
model = sm.OLS(data_yX.iloc[:, 0], data_yX.iloc[:, 1:])
result = model.fit()
print('\n取对数后的多元线性回归模型的构建:\n', result.summary())
# 异方差检验
het_white = sm.stats.diagnostic.het_white(residuals, result.model.exog)
print('\n异方差检验:\nWhite检验统计量:', het_white[0])
print('White检验p值:', het_white[1])
result = model.fit(cov_type='HAC', cov_kwds={'maxlags': 1})
result = result.get_robustcov_results(cov_type='HC3')
print('\n使用标准误修正异方差后的多元线性回归模型的构建:\n', result.summary())
plt.show()