Statsmodels库的学习历程:因子分析
1.问题引入
粮食产量的影响因素有很多,现从粮食作物播种面积、有效灌溉面积、农用化肥施用折纯量、农业机械总动力、农村用电量、成灾面积这6个指标着手分析,具体数据如下所示:
年份 粮食产量(万吨) 粮食作物播种面积(千公顷) 有效灌溉面积(千公顷) 农用化肥施用折纯量(万吨) 农业机械总动力(万千瓦) 农村用电量(亿千瓦小时) 成灾面积(千公顷)
1991 43529.3 112313.6 47822.07 2805.1 29388.6 963.2 27810
1992 44265.8 110559.7 48590.1 2930.2 30308.4 1107.1 25900
1993 45648.8 110508.7 48727.9 3151.9 31816.6 1244.9 23130
1994 44510.1 109543.7 48759.1 3317.9 33802.5 1473.9 31380
1995 46661.8 110060.4 49281.2 3593.7 36118.05 1655.66 22270
1996 50453.5 112547.92 50381.4 3827.93 38546.92 1812.7 21230
1997 49417.1 112912.1 51238.5 3980.7 42015.64 1980.1 30310
1998 51229.53 113787.4 52295.6 4085.6 45207.71 2042.1 25180
1999 50838.58 113160.98 53158.41 4124.32 48996.12 2173.4 26730
2000 46217.52 108462.54 53820.33 4146.41 52573.61 2421.3 34370
2001 45263.67 106080.04 54249.39 4253.76 55172.1 2610.8 31790
2002 45705.75 103890.83 54354.85 4339.39 57929.85 2993.4 27160
2003 43069.53 99410.37 54014.23 4411.56 60386.54 3432.9 32520
2004 46946.95 101606.03 54478.42 4636.58 64027.91 3933 16300
2005 48402.19 104278.38 55029.34 4766.22 68397.85 4375.7 19970
2006 49804.23 104957.7 55750.5 4927.69 72522.12 4895.82 24630
2007 50413.85 105998.62 56518.34 5107.83 76589.56 5509.93 25060
2008 53434.29 107544.51 58471.68 5239.02 82190.41 5713.15 22280
2009 53940.86 110255.09 59261.45 5404.35 87496.1 6104.44 21230
2010 55911.31 111695.42 60347.7 5561.68 92780.48 6632.35 18540
2011 58849.33 112980.35 61681.56 5704.24 97734.66 7139.62 12440
2012 61222.62 114368.04 62490.52 5838.85 102558.96 7508.46 11470
2013 63048.2 115907.54 63473.3 5911.86 103906.75 8549.52 14300
2014 63964.83 117455.18 64539.53 5995.94 108056.58 8884.45 12680
2015 66060.27 118962.81 65872.64 6022.6 111728.07 9026.92 12380
2016 66043.51 119230.06 67140.62 5984.41 97245.59 9238.26 13670
2017 66160.73 117989.06 67815.57 5859.41 98783.35 9524.42 9200
2018 65789.22 117038.21 68271.64 5653.42 100371.74 9358.54 10569
2019 66384.34 116063.6 68678.61 5403.59 102758.26 9482.87 7913
2020 66949.15 116768.17 69160.52 5250.65 105622.15 6210.98 7993
2021 68284.75 117630.82 69609.48 5191.26 107764.32 6736.3 4682
2022 68652.77 118332.11 70358.87 5079.2 110597.19 7765.57 4373
2023 69540.99 118968.54 71644 5021.74 113742.57 7991.9 4797
数据下载地址:
https://data.stats.gov.cn/easyquery.htm?cn=C01
2.因子分析
2.1.标准化/归一化处理
由于各指标的量纲不同(单位不一致),因此,需要对数据(除了因变量:粮食产量)进行标准化/归一化处理,输出结果如下:
粮食作物播种面积(千公顷) 有效灌溉面积(千公顷) 农用化肥施用折纯量(万吨) 农业机械总动力(万千瓦) 农村用电量(亿千瓦小时) 成灾面积(千公顷)
年份
1991 0.651031 0.000000 0.000000 0.000000 0.000000 0.781311
1992 0.562538 0.032240 0.038881 0.010904 0.016808 0.717638
1993 0.559965 0.038025 0.107786 0.028783 0.032904 0.625296
1994 0.511276 0.039335 0.159378 0.052326 0.059653 0.900323
1995 0.537346 0.061252 0.245097 0.079776 0.080883 0.596626
1996 0.662853 0.107436 0.317896 0.108570 0.099227 0.561956
1997 0.681228 0.143415 0.365377 0.149691 0.118780 0.864653
1998 0.725391 0.187790 0.397980 0.187532 0.126022 0.693636
1999 0.693785 0.224010 0.410014 0.232443 0.141358 0.745308
2000 0.456726 0.251796 0.416880 0.274854 0.170315 1.000000
2001 0.336517 0.269807 0.450244 0.305658 0.192449 0.913991
2002 0.226061 0.274234 0.476858 0.338351 0.237139 0.759643
2003 0.000000 0.259935 0.499288 0.367475 0.288475 0.938327
2004 0.110782 0.279421 0.569225 0.410642 0.346890 0.397606
2005 0.245615 0.302548 0.609517 0.462447 0.398600 0.519952
2006 0.279890 0.332821 0.659702 0.511340 0.459353 0.675301
2007 0.332409 0.365053 0.715689 0.559558 0.531084 0.689636
2008 0.410407 0.447051 0.756463 0.625955 0.554822 0.596960
2009 0.547169 0.480204 0.807848 0.688853 0.600527 0.561956
2010 0.619841 0.525802 0.856746 0.751498 0.662190 0.472281
2011 0.684672 0.581795 0.901054 0.810229 0.721442 0.268927
2012 0.754687 0.615754 0.942890 0.867420 0.764524 0.236590
2013 0.832363 0.657009 0.965582 0.883398 0.886126 0.330933
2014 0.910449 0.701768 0.991714 0.932594 0.925248 0.276928
2015 0.986516 0.757729 1.000000 0.976118 0.941889 0.266927
2016 1.000000 0.810957 0.988131 0.804431 0.966575 0.309931
2017 0.937385 0.839290 0.949280 0.822661 1.000000 0.160916
2018 0.889410 0.858435 0.885259 0.841491 0.980624 0.206554
2019 0.840237 0.875518 0.807611 0.869783 0.995147 0.118012
2020 0.875786 0.895748 0.760078 0.903734 0.612971 0.120679
2021 0.919311 0.914595 0.741619 0.929129 0.674331 0.010301
2022 0.954694 0.946053 0.706791 0.962712 0.794556 0.000000
2023 0.986805 1.000000 0.688932 1.000000 0.820993 0.014135
2.2.皮尔逊相关性分析
通过计算指标之间的线性相关性,了解指标之间的相关性强弱,有助于确定因子个数和处理可能存在的共线性问题,如果相关性矩阵中大部分相关系数小于0.3且未通过充分性检验(KMO检验和Bartlett检验),则不适用于因子分析。构造皮尔逊相关性矩阵,输出结果如下所示:
粮食作物播种面积(千公顷) 有效灌溉面积(千公顷) 农用化肥施用折纯量(万吨) 农业机械总动力(万千瓦) 农村用电量(亿千瓦小时) 成灾面积(千公顷)
粮食作物播种面积(千公顷) 1.000000 0.664195 0.419743 0.554409 0.587688 -0.705074
有效灌溉面积(千公顷) 0.664195 1.000000 0.835334 0.958938 0.927282 -0.879490
农用化肥施用折纯量(万吨) 0.419743 0.835334 1.000000 0.928487 0.935114 -0.678662
农业机械总动力(万千瓦) 0.554409 0.958938 0.928487 1.000000 0.956195 -0.835930
农村用电量(亿千瓦小时) 0.587688 0.927282 0.935114 0.956195 1.000000 -0.813051
成灾面积(千公顷) -0.705074 -0.879490 -0.678662 -0.835930 -0.813051 1.000000
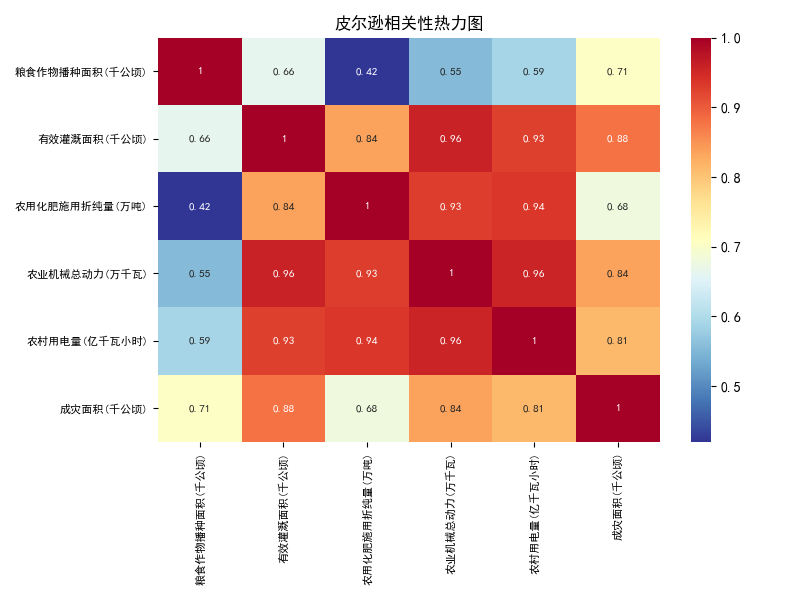
绘制皮尔逊相关性热力图,输出结果如下所示:
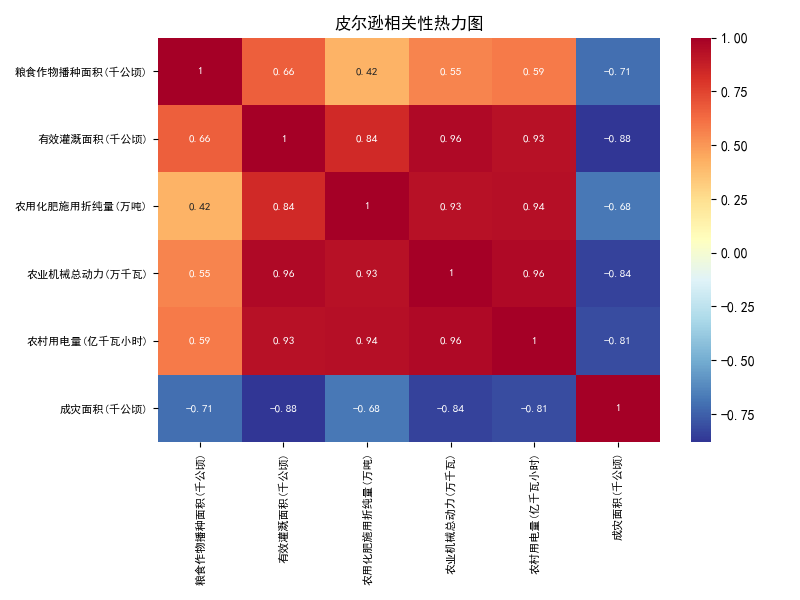
由上述结果可知,各项指标之间存在高度相关性,初步判断能够做因子分析。
2.3.充分性检验(KMO检验和Bartlett检验)
KMO检验: KMO值介于0和1之间,如果全部变量间相关系数平方和远大于偏相关系数平方和则KMO值接近1,KMO值越接近1越适合作因子分析。一般情况下,当KMO值大于0.6(严格一点就以0.7为阈值进行判断)时,表示指标之间的相关性较强,偏相关性较弱,适合做因子分析。
Bartlett检验: 原假设相关系数矩阵为单位阵,若得到的概率值小于规定的显著性水平(一般取0.05,严格一点就以0.01为阈值进行判断)则拒绝原假设,认为数据适合做因子分析,通俗来讲,即显著性水平越趋近于0则越适合做因子分析,反之则不能拒绝原假设,即数据不适合做因子分析。
KMO检验和Bartlett检验输出结果如下所示:
KMO检验: 0.8086986235906963
Bartlett检验: 5.179399618417234e-55
由上述结果可知,KMO值为0.81,大于0.6的阈值,通过了KMO检验;Bartlett检验的p值也趋近于0,通过了Bartlett检验。综上,可以做因子分析。
2.4.构造载荷矩阵
构造载荷矩阵并对其进行旋转,输出结果如下所示:
旋转前载荷矩阵的贡献率:
旋转前特征根 旋转前方差贡献率 旋转前方差累计贡献率
0 4.942224 0.823704 0.823704
1 0.704599 0.117433 0.941137
2 0.219033 0.036506 0.977643
3 0.081300 0.013550 0.991193
4 0.038707 0.006451 0.997644
5 0.014137 0.002356 1.000000
旋转后载荷矩阵的贡献率:
旋转后特征根 旋转后方差贡献率 旋转后方差累计贡献率
0 3.113324 0.518887 0.518887
1 1.397528 0.232921 0.751809
2 1.355005 0.225834 0.977643
绘制碎石图,输出结果如下所示:
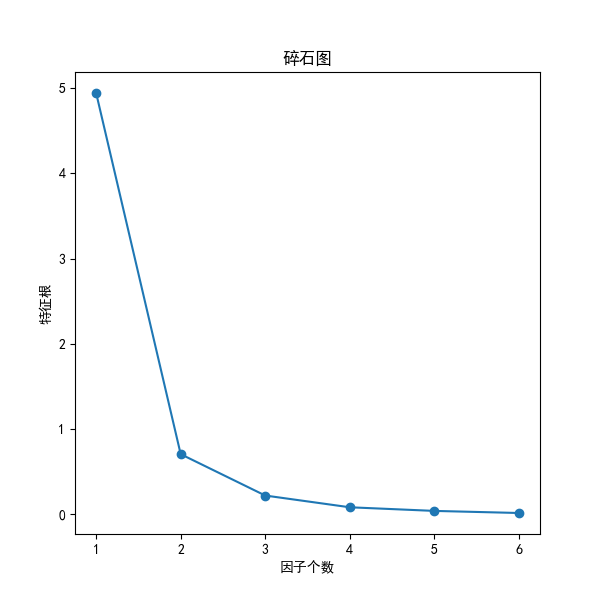
由上述结果可知,提取3个成分因子能够解释因变量(粮食产量)变动情况的97.76%,因此,决定提取的成分因子个数为3。
2.5.构造公因子方差表
构造公因子方差表,输出结果如下所示:
提取
粮食作物播种面积(千公顷) 0.999408
有效灌溉面积(千公顷) 0.954335
农用化肥施用折纯量(万吨) 0.978055
农业机械总动力(万千瓦) 0.980913
农村用电量(亿千瓦小时) 0.971017
成灾面积(千公顷) 0.982129
构造公因子方差表是为了了解各原始指标之间的共同度,即各原始指标能被提取出的程度,由上述结果可知,所有指标的共同度都在0.95以上,说明因子能解释指标中的大部分信息,验证了这些指标适合进行因子分析。
2.6.构造成分矩阵
构造成分矩阵,输出结果如下所示:
成分因子1 成分因子2 成分因子3
粮食作物播种面积(千公顷) 0.225064 0.936841 0.266616
有效灌溉面积(千公顷) 0.716262 0.386172 0.540533
农用化肥施用折纯量(万吨) 0.953647 0.156221 0.210254
农业机械总动力(万千瓦) 0.837483 0.258106 0.461428
农村用电量(亿千瓦小时) 0.855756 0.319432 0.369678
成灾面积(千公顷) 0.454421 0.421508 0.773279
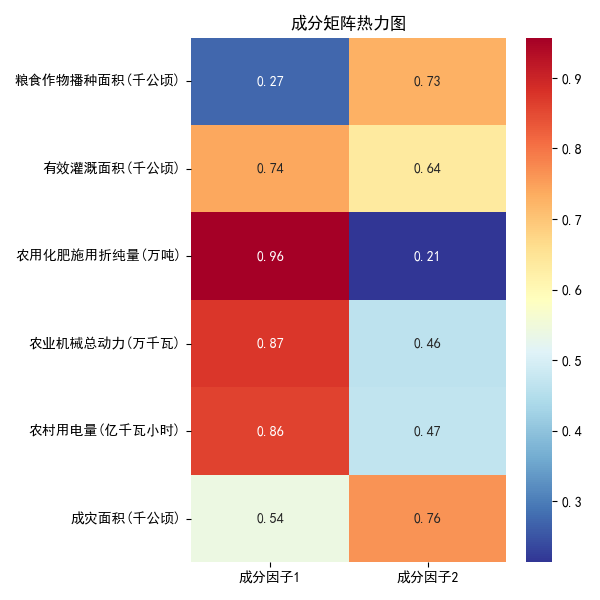
绘制成分矩阵热力图,输出结果如下所示:
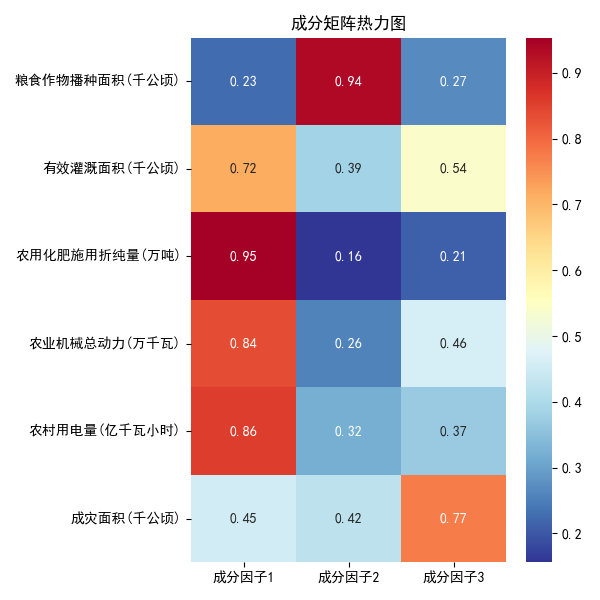
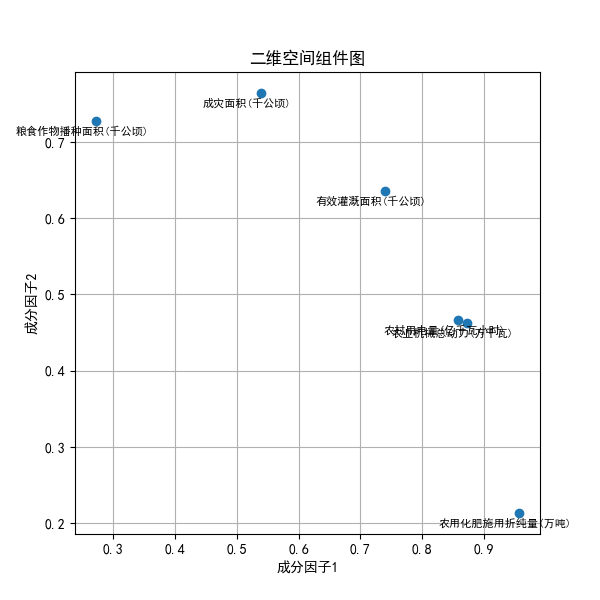
绘制成分矩阵三维空间组件图,输出结果如下所示:
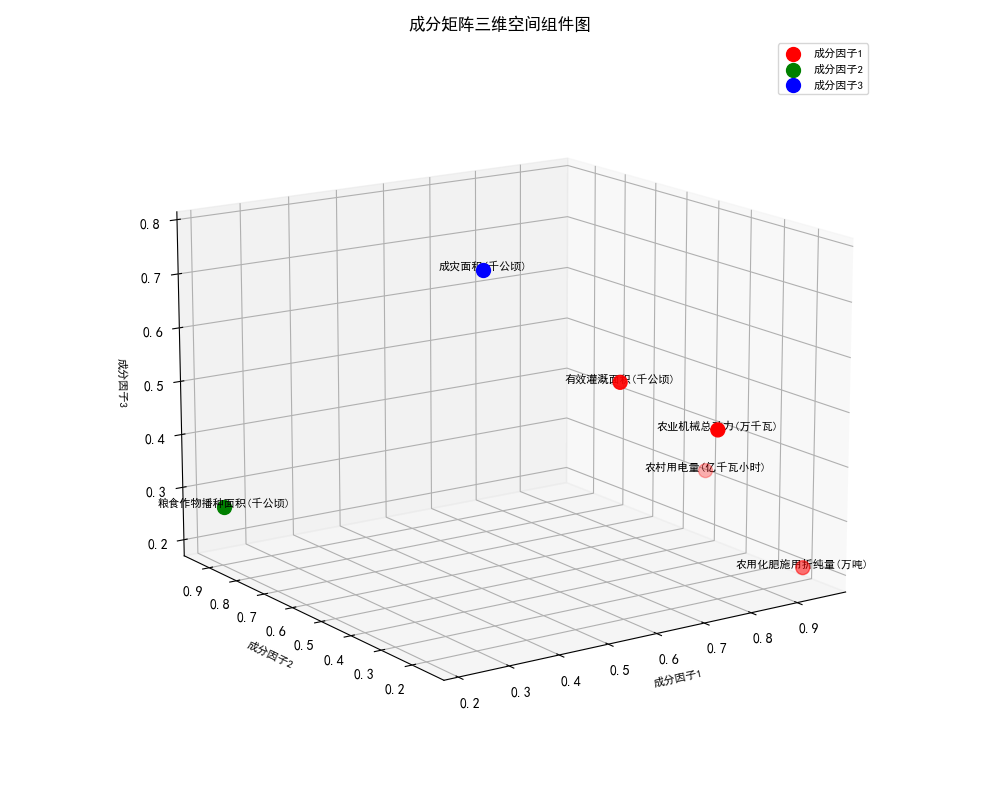
由上述成分矩阵可知,成分因子1主要解释有效灌溉面积、农用化肥施用折纯量、农业机械总动力、农村用电量这4个指标,可定义为农业技术装备因子;成分因子2主要解释粮食作物播种面积这1个指标,可定义为粮食生产规模因子,成分因子3主要解释成灾面积这1个指标,可定义为农业灾害风险因子。

2.7.计算因子得分
计算因子得分,输出结果如下所示:
成分因子1 成分因子2 成分因子3
年份
1991 -2.022990 0.702103 -0.385575
1992 -1.978190 0.208525 0.087849
1993 -1.944238 0.087483 0.392477
1994 -1.250554 0.150589 -1.025624
1995 -1.555512 -0.073683 0.261248
1996 -1.440549 0.455867 0.005088
1997 -0.722983 0.846933 -1.649436
1998 -0.928404 0.840904 -0.903454
1999 -0.735911 0.721916 -1.066720
2000 -0.094965 -0.133923 -1.770902
2001 -0.071991 -0.806934 -1.106843
2002 -0.167044 -1.503019 -0.137163
2003 0.380240 -2.371736 -0.598087
2004 -0.370816 -2.457809 1.699561
2005 0.001250 -1.714420 0.657782
2006 0.505205 -1.405033 -0.331065
2007 0.772559 -1.161940 -0.669175
2008 0.762411 -0.942763 -0.377776
2009 0.877454 -0.370508 -0.630315
2010 0.931784 -0.157740 -0.440075
2011 0.766762 -0.105935 0.371789
2012 0.881719 0.158670 0.292930
2013 1.238629 0.630751 -0.472352
2014 1.263414 0.911139 -0.407925
2015 1.296164 1.227094 -0.487376
2016 1.242605 1.418590 -0.734436
2017 0.958324 0.954463 0.288913
2018 0.898398 0.763639 0.382266
2019 0.608885 0.422724 1.168222
2020 0.064483 0.505105 1.538084
2021 -0.103637 0.583520 2.023814
2022 -0.049478 0.736821 2.033477
2023 -0.013026 0.878606 1.990798
2.8.计算综合得分
综合得分的计算公式为: $$ \text{F}\left( \text{综合} \right) =\frac{0.52\text{F}1+0.23\text{F}2+0.23\text{F}3}{0.98} $$ 值得注意的是,0.52、0.23、0.23分别为各成分因子的方差贡献率,0.98为累计方差贡献率。
综合得分输出结果如下所示:
粮食产量(万吨) 成分因子1 成分因子2 成分因子3 综合得分
年份
1991 43529.30 -2.022990 0.702103 -0.385575 -0.995501
1992 44265.80 -1.978190 0.208525 0.087849 -0.979957
1993 45648.80 -1.944238 0.087483 0.392477 -0.920407
1994 44510.10 -1.250554 0.150589 -1.025624 -0.864776
1995 46661.80 -1.555512 -0.073683 0.261248 -0.782800
1996 50453.50 -1.440549 0.455867 0.005088 -0.654792
1997 49417.10 -0.722983 0.846933 -1.649436 -0.562963
1998 51229.53 -0.928404 0.840904 -0.903454 -0.501106
1999 50838.58 -0.735911 0.721916 -1.066720 -0.465003
2000 46217.52 -0.094965 -0.133923 -1.770902 -0.491385
2001 45263.67 -0.071991 -0.806934 -1.106843 -0.486139
2002 45705.75 -0.167044 -1.503019 -0.137163 -0.478435
2003 43069.53 0.380240 -2.371736 -0.598087 -0.501405
2004 46946.95 -0.370816 -2.457809 1.699561 -0.389784
2005 48402.19 0.001250 -1.714420 0.657782 -0.255847
2006 49804.23 0.505205 -1.405033 -0.331065 -0.143083
2007 50413.85 0.772559 -1.161940 -0.669175 -0.021370
2008 53434.29 0.762411 -0.942763 -0.377776 0.092775
2009 53940.86 0.877454 -0.370508 -0.630315 0.231837
2010 55911.31 0.931784 -0.157740 -0.440075 0.355310
2011 58849.33 0.766762 -0.105935 0.371789 0.467606
2012 61222.62 0.881719 0.158670 0.292930 0.573445
2013 63048.20 1.238629 0.630751 -0.472352 0.698569
2014 63964.83 1.263414 0.911139 -0.407925 0.793408
2015 66060.27 1.296164 1.227094 -0.487376 0.867713
2016 66043.51 1.242605 1.418590 -0.734436 0.827840
2017 66160.73 0.958324 0.954463 0.288913 0.802771
2018 65789.22 0.898398 0.763639 0.382266 0.747066
2019 66384.34 0.608885 0.422724 1.168222 0.693739
2020 66949.15 0.064483 0.505105 1.538084 0.509860
2021 68284.75 -0.103637 0.583520 2.023814 0.551515
2022 68652.77 -0.049478 0.736821 2.033477 0.619016
2023 69540.99 -0.013026 0.878606 1.990798 0.662284
由上述结果可知,随着年份的增加,综合得分也越来越高,说明粮食产量逐年变多,粮食生产的态势逐年变好。
3.python程序
3.1.python程序一
上述案例所使用的是该程序,主要通过调用factor_analyzer库来进行因子分析,具体程序如下所示:
import pandas as pd
import numpy as np
from sklearn.preprocessing import MinMaxScaler
from factor_analyzer import FactorAnalyzer, calculate_kmo, calculate_bartlett_sphericity
import matplotlib.pyplot as plt
import seaborn as sns
# 忽略警告
import warnings
warnings.filterwarnings("ignore")
# 绘图时正常显示中文
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 显示所有列
pd.set_option('display.max_columns', None)
# 禁止换行
pd.set_option('expand_frame_repr', False)
# 读取数据
data = pd.read_excel(io='数据.xlsx', index_col=0)
print('原始数据:\n', data)
# 数据标准化处理
data_std = pd.DataFrame(MinMaxScaler().fit_transform(data.iloc[:, 1:]), index=data.index, columns=data.columns[1:])
print('\n标准化处理后的数据:\n', data_std)
# 构造皮尔逊相关性矩阵
data_corr = data_std.corr(method='pearson')
print('\n皮尔逊相关性矩阵:\n', data_corr)
# 绘制皮尔逊相关性热力图
plt.figure(figsize=(8, 6))
sns.heatmap(data_corr, cmap='RdYlBu_r', annot=True, annot_kws={'fontsize': 8})
plt.xticks(fontsize=8)
plt.yticks(fontsize=8)
plt.title('皮尔逊相关性热力图')
plt.tight_layout()
# KMO检验和Bartlett检验
kmo = calculate_kmo(data_std) # KMO>0.6,则通过KMO检验
bartlett = calculate_bartlett_sphericity(data_std) # Bartlett<0.05,则通过Bartlett检验
print('\nKMO检验:', kmo[1], '\nBartlett检验:', bartlett[1])
# 旋转前载荷矩阵
matrix = FactorAnalyzer(rotation=None, n_factors=data_std.shape[1], method='principal')
matrix.fit(data_std)
f_contribution_var = matrix.get_factor_variance()
matrices_var = pd.DataFrame()
matrices_var["旋转前特征根"] = f_contribution_var[0]
matrices_var["旋转前方差贡献率"] = f_contribution_var[1]
matrices_var["旋转前方差累计贡献率"] = f_contribution_var[2]
print('\n旋转前载荷矩阵的贡献率:\n', matrices_var)
# 旋转后载荷矩阵
n_factors = 3
matrix_rotated = FactorAnalyzer(rotation='varimax', n_factors=n_factors, method='principal')
matrix_rotated.fit(data_std)
f_contribution_var_rotated = matrix_rotated.get_factor_variance()
matrices_var_rotated = pd.DataFrame()
matrices_var_rotated["旋转后特征根"] = f_contribution_var_rotated[0]
matrices_var_rotated["旋转后方差贡献率"] = f_contribution_var_rotated[1]
matrices_var_rotated["旋转后方差累计贡献率"] = f_contribution_var_rotated[2]
print('\n旋转后载荷矩阵的贡献率:\n', matrices_var_rotated)
# 构造公因子方差表
communalities = pd.DataFrame(matrix_rotated.get_communalities(), index=data_std.columns, columns=['提取'])
print('\n公因子方差表:\n', communalities)
# 绘制碎石图
ev, v = matrix_rotated.get_eigenvalues()
plt.figure(figsize=(6, 6))
plt.scatter(range(1, data_std.shape[1] + 1), ev)
plt.plot(range(1, data_std.shape[1] + 1), ev)
plt.title('碎石图')
plt.xlabel('因子个数')
plt.ylabel('特征根')
# 绘制成分矩阵热力图
component_matrix = pd.DataFrame(np.abs(matrix_rotated.loadings_), index=data_std.columns,
columns=[f'成分因子{i + 1}' for i in range(n_factors)])
print('\n成分矩阵:\n', component_matrix)
plt.figure(figsize=(6, 6))
sns.heatmap(component_matrix, annot=True, cmap='RdYlBu_r')
plt.title('成分矩阵热力图')
plt.tight_layout()
# # 绘制成分矩阵二维空间组件图
# plt.figure(figsize=(6, 6))
# x = component_matrix.iloc[:, 0]
# y = component_matrix.iloc[:, 1]
# plt.scatter(x, y)
# for i in range(len(component_matrix)):
# plt.annotate(component_matrix.index[i], (x[i], y[i]), textcoords='offset points', xytext=(-10, -10), ha='center',
# fontsize=8)
# plt.xlabel(component_matrix.columns[0])
# plt.ylabel(component_matrix.columns[1])
# plt.title('二维空间组件图')
# plt.grid(True)
# 绘制成分矩阵三维空间组件图
groups = np.argmax(np.array(component_matrix), axis=1)
colors = ['r', 'g', 'b']
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
for i in range(3):
mask = groups == i
ax.scatter(np.array(component_matrix)[mask, 0],
np.array(component_matrix)[mask, 1],
np.array(component_matrix)[mask, 2],
c=colors[i], s=100, label=f'成分因子{i + 1}')
for i, (x, y, z) in enumerate(np.array(component_matrix)):
ax.text(x, y, z, component_matrix.index[i], fontsize=8, ha='center')
ax.set_xlabel('成分因子1', fontsize=8)
ax.set_ylabel('成分因子2', fontsize=8)
ax.set_zlabel('成分因子3', fontsize=8)
ax.set_title('成分矩阵三维空间组件图', fontsize=12)
ax.legend(fontsize=8)
plt.tight_layout()
# 计算因子得分
factor_score = pd.DataFrame(matrix_rotated.transform(data_std), index=data.index,
columns=[f'成分因子{i + 1}' for i in range(n_factors)])
print('\n因子得分:\n', factor_score)
# 计算综合得分
weight = matrices_var_rotated["旋转后方差贡献率"] / np.sum(matrices_var_rotated["旋转后方差贡献率"])
factor_score["综合得分"] = np.dot(factor_score, weight)
factor_score = pd.concat([data.iloc[:, 0], factor_score], axis=1)
print('\n综合得分:\n', factor_score)
# 保存综合得分到新的excel
factor_score.to_excel('综合得分.xlsx')
plt.show()
3.2.python程序二
上述案例并没有使用该程序,主要通过调用statsmodels库来进行因子分析,但得到的结果并不理想,具体程序如下所示:
import pandas as pd
import numpy as np
from sklearn.preprocessing import MinMaxScaler
from factor_analyzer import calculate_kmo, calculate_bartlett_sphericity
from statsmodels.multivariate.factor import Factor
import matplotlib.pyplot as plt
import seaborn as sns
# 忽略警告
import warnings
warnings.filterwarnings("ignore")
# 绘图时正常显示中文
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 显示所有列
pd.set_option('display.max_columns', None)
# 禁止换行
pd.set_option('expand_frame_repr', False)
# 读取数据
data = pd.read_excel(io='数据.xlsx', index_col=0)
print('原始数据:\n', data)
# 数据标准化处理
def directional_normalization(data, directions):
processed_data = data.copy().astype(float)
for i, direction in enumerate(directions):
if direction == -1:
processed_data[:, i] = np.max(data[:, i]) - data[:, i]
scaler = MinMaxScaler()
normalized_data = scaler.fit_transform(processed_data)
return normalized_data
directions = [1, 1, 1, 1, 1, -1] # 区分正向指标和负向指标
data_std = directional_normalization(np.array(data.iloc[:, 1:]), directions)
data_std = pd.DataFrame(data_std, index=data.index, columns=data.columns[1:])
print('\n标准化处理后的数据:\n', data_std)
# 构造皮尔逊相关性矩阵
data_corr = data_std.corr(method='pearson')
print('\n皮尔逊相关性矩阵:\n', data_corr)
# 绘制皮尔逊相关性热力图
plt.figure(figsize=(8, 6))
sns.heatmap(data_corr, cmap='RdYlBu_r', annot=True, annot_kws={'fontsize': 8})
plt.xticks(fontsize=8)
plt.yticks(fontsize=8)
plt.title('皮尔逊相关性热力图')
plt.tight_layout()
# KMO检验和Bartlett检验
kmo = calculate_kmo(data_std) # KMO>0.6,则通过KMO检验
bartlett = calculate_bartlett_sphericity(data_std) # Bartlett<0.05,则通过Bartlett检验
print('\nKMO检验:', kmo[1], '\nBartlett检验:', bartlett[1])
# 因子分析结果
n_factor = 2
factor = Factor(endog=data_std, n_factor=n_factor, method='pa') # 主轴因子分析(PA),最大似然估计(ML)
result = factor.fit()
result.rotate(method='varimax')
print('\n因子分析结果:\n', result.summary())
eigenvalues = result.eigenvals[:n_factor]
total_variance = np.sum(eigenvalues)
variance_ratio = eigenvalues / total_variance
cumulative_ratio = np.cumsum(variance_ratio)
contribution = pd.DataFrame({
'特征根': eigenvalues,
'方差贡献率': variance_ratio,
'累计方差贡献率': cumulative_ratio
})
print('\n总方差解释表:\n', contribution)
# 绘制成分矩阵热力图
component_matrix = pd.DataFrame(np.abs(result.loadings), index=data_std.columns,
columns=[f'成分因子{i + 1}' for i in range(n_factor)])
print('\n成分矩阵:\n', component_matrix)
plt.figure(figsize=(6, 6))
sns.heatmap(component_matrix, annot=True, cmap='RdYlBu_r')
plt.title('成分矩阵热力图')
plt.tight_layout()
# 绘制成分矩阵二维空间组件图
plt.figure(figsize=(6, 6))
x = component_matrix.iloc[:, 0]
y = component_matrix.iloc[:, 1]
plt.scatter(x, y)
for i in range(len(component_matrix)):
plt.annotate(component_matrix.index[i], (x[i], y[i]), textcoords='offset points', xytext=(-10, -10), ha='center',
fontsize=8)
plt.xlabel(component_matrix.columns[0])
plt.ylabel(component_matrix.columns[1])
plt.title('二维空间组件图')
plt.grid(True)
# 计算因子得分
factor_score = pd.DataFrame(result.factor_scoring(method='bartlett'), index=data.index,
columns=[f'成分因子{i + 1}' for i in range(n_factor)])
print('\n因子得分:\n', factor_score)
# 计算综合得分
weight = variance_ratio / np.sum(variance_ratio)
factor_score["综合得分"] = np.dot(factor_score, weight)
factor_score = pd.concat([data.iloc[:, 0], factor_score], axis=1)
print('\n综合得分:\n', factor_score)
# 保存综合得分到新的excel
factor_score.to_excel('综合得分.xlsx')
plt.show()
输出结果如下所示:
原始数据:
粮食产量(万吨) 粮食作物播种面积(千公顷) 有效灌溉面积(千公顷) 农用化肥施用折纯量(万吨) 农业机械总动力(万千瓦) 农村用电量(亿千瓦小时) 成灾面积(千公顷)
年份
1991 43529.30 112313.60 47822.07 2805.10 29388.60 963.20 27810
1992 44265.80 110559.70 48590.10 2930.20 30308.40 1107.10 25900
1993 45648.80 110508.70 48727.90 3151.90 31816.60 1244.90 23130
1994 44510.10 109543.70 48759.10 3317.90 33802.50 1473.90 31380
1995 46661.80 110060.40 49281.20 3593.70 36118.05 1655.66 22270
1996 50453.50 112547.92 50381.40 3827.93 38546.92 1812.70 21230
1997 49417.10 112912.10 51238.50 3980.70 42015.64 1980.10 30310
1998 51229.53 113787.40 52295.60 4085.60 45207.71 2042.10 25180
1999 50838.58 113160.98 53158.41 4124.32 48996.12 2173.40 26730
2000 46217.52 108462.54 53820.33 4146.41 52573.61 2421.30 34370
2001 45263.67 106080.04 54249.39 4253.76 55172.10 2610.80 31790
2002 45705.75 103890.83 54354.85 4339.39 57929.85 2993.40 27160
2003 43069.53 99410.37 54014.23 4411.56 60386.54 3432.90 32520
2004 46946.95 101606.03 54478.42 4636.58 64027.91 3933.00 16300
2005 48402.19 104278.38 55029.34 4766.22 68397.85 4375.70 19970
2006 49804.23 104957.70 55750.50 4927.69 72522.12 4895.82 24630
2007 50413.85 105998.62 56518.34 5107.83 76589.56 5509.93 25060
2008 53434.29 107544.51 58471.68 5239.02 82190.41 5713.15 22280
2009 53940.86 110255.09 59261.45 5404.35 87496.10 6104.44 21230
2010 55911.31 111695.42 60347.70 5561.68 92780.48 6632.35 18540
2011 58849.33 112980.35 61681.56 5704.24 97734.66 7139.62 12440
2012 61222.62 114368.04 62490.52 5838.85 102558.96 7508.46 11470
2013 63048.20 115907.54 63473.30 5911.86 103906.75 8549.52 14300
2014 63964.83 117455.18 64539.53 5995.94 108056.58 8884.45 12680
2015 66060.27 118962.81 65872.64 6022.60 111728.07 9026.92 12380
2016 66043.51 119230.06 67140.62 5984.41 97245.59 9238.26 13670
2017 66160.73 117989.06 67815.57 5859.41 98783.35 9524.42 9200
2018 65789.22 117038.21 68271.64 5653.42 100371.74 9358.54 10569
2019 66384.34 116063.60 68678.61 5403.59 102758.26 9482.87 7913
2020 66949.15 116768.17 69160.52 5250.65 105622.15 6210.98 7993
2021 68284.75 117630.82 69609.48 5191.26 107764.32 6736.30 4682
2022 68652.77 118332.11 70358.87 5079.20 110597.19 7765.57 4373
2023 69540.99 118968.54 71644.00 5021.74 113742.57 7991.90 4797
标准化处理后的数据:
粮食作物播种面积(千公顷) 有效灌溉面积(千公顷) 农用化肥施用折纯量(万吨) 农业机械总动力(万千瓦) 农村用电量(亿千瓦小时) 成灾面积(千公顷)
年份
1991 0.651031 0.000000 0.000000 0.000000 0.000000 0.218689
1992 0.562538 0.032240 0.038881 0.010904 0.016808 0.282362
1993 0.559965 0.038025 0.107786 0.028783 0.032904 0.374704
1994 0.511276 0.039335 0.159378 0.052326 0.059653 0.099677
1995 0.537346 0.061252 0.245097 0.079776 0.080883 0.403374
1996 0.662853 0.107436 0.317896 0.108570 0.099227 0.438044
1997 0.681228 0.143415 0.365377 0.149691 0.118780 0.135347
1998 0.725391 0.187790 0.397980 0.187532 0.126022 0.306364
1999 0.693785 0.224010 0.410014 0.232443 0.141358 0.254692
2000 0.456726 0.251796 0.416880 0.274854 0.170315 0.000000
2001 0.336517 0.269807 0.450244 0.305658 0.192449 0.086009
2002 0.226061 0.274234 0.476858 0.338351 0.237139 0.240357
2003 0.000000 0.259935 0.499288 0.367475 0.288475 0.061673
2004 0.110782 0.279421 0.569225 0.410642 0.346890 0.602394
2005 0.245615 0.302548 0.609517 0.462447 0.398600 0.480048
2006 0.279890 0.332821 0.659702 0.511340 0.459353 0.324699
2007 0.332409 0.365053 0.715689 0.559558 0.531084 0.310364
2008 0.410407 0.447051 0.756463 0.625955 0.554822 0.403040
2009 0.547169 0.480204 0.807848 0.688853 0.600527 0.438044
2010 0.619841 0.525802 0.856746 0.751498 0.662190 0.527719
2011 0.684672 0.581795 0.901054 0.810229 0.721442 0.731073
2012 0.754687 0.615754 0.942890 0.867420 0.764524 0.763410
2013 0.832363 0.657009 0.965582 0.883398 0.886126 0.669067
2014 0.910449 0.701768 0.991714 0.932594 0.925248 0.723072
2015 0.986516 0.757729 1.000000 0.976118 0.941889 0.733073
2016 1.000000 0.810957 0.988131 0.804431 0.966575 0.690069
2017 0.937385 0.839290 0.949280 0.822661 1.000000 0.839084
2018 0.889410 0.858435 0.885259 0.841491 0.980624 0.793446
2019 0.840237 0.875518 0.807611 0.869783 0.995147 0.881988
2020 0.875786 0.895748 0.760078 0.903734 0.612971 0.879321
2021 0.919311 0.914595 0.741619 0.929129 0.674331 0.989699
2022 0.954694 0.946053 0.706791 0.962712 0.794556 1.000000
2023 0.986805 1.000000 0.688932 1.000000 0.820993 0.985865
皮尔逊相关性矩阵:
粮食作物播种面积(千公顷) 有效灌溉面积(千公顷) 农用化肥施用折纯量(万吨) 农业机械总动力(万千瓦) 农村用电量(亿千瓦小时) 成灾面积(千公顷)
粮食作物播种面积(千公顷) 1.000000 0.664195 0.419743 0.554409 0.587688 0.705074
有效灌溉面积(千公顷) 0.664195 1.000000 0.835334 0.958938 0.927282 0.879490
农用化肥施用折纯量(万吨) 0.419743 0.835334 1.000000 0.928487 0.935114 0.678662
农业机械总动力(万千瓦) 0.554409 0.958938 0.928487 1.000000 0.956195 0.835930
农村用电量(亿千瓦小时) 0.587688 0.927282 0.935114 0.956195 1.000000 0.813051
成灾面积(千公顷) 0.705074 0.879490 0.678662 0.835930 0.813051 1.000000
KMO检验: 0.8086986235906976
Bartlett检验: 5.179399618416939e-55
因子分析结果:
Factor analysis results
============================================================================
Eigenvalues
----------------------------------------------------------------------------
粮食作物播种面积(千公顷) 有效灌溉面积(千公顷) 农用化肥施用折纯量(万吨) 农业机械总动力(万千瓦) 农村用电量(亿千瓦小时) 成灾面积(千公顷)
----------------------------------------------------------------------------
4.8564 0.4688 0.0424 0.0067 -0.0166 -0.0325
----------------------------------------------------------------------------
----------------------------------------------------------------------------
Communality
----------------------------------------------------------------------------
粮食作物播种面积(千公顷) 有效灌溉面积(千公顷) 农用化肥施用折纯量(万吨) 农业机械总动力(万千瓦) 农村用电量(亿千瓦小时) 成灾面积(千公顷)
----------------------------------------------------------------------------
0.6040 0.9521 0.9618 0.9765 0.9560 0.8748
----------------------------------------------------------------------------
----------------------------------------------------------------------------
Pre-rotated loadings
-------------------------------------------------------------------------------------------------------------------------
factor 0 factor 1
-------------------------------------------------------------------------------------------------------------------------
粮食作物播种面积(千公顷) 0.6490 -0.4275
有效灌溉面积(千公顷) 0.9727 -0.0767
农用化肥施用折纯量(万吨) 0.8989 0.3922
农业机械总动力(万千瓦) 0.9780 0.1414
农村用电量(亿千瓦小时) 0.9691 0.1302
成灾面积(千公顷) 0.8862 -0.2990
----------------------------------------------------------------------------
----------------------------------------------------------------------------
varimax rotated loadings
-------------------------------------------------------------------------------------------------------------------------
factor 0 factor 1
-------------------------------------------------------------------------------------------------------------------------
粮食作物播种面积(千公顷) 0.2720 -0.7280
有效灌溉面积(千公顷) 0.7403 -0.6357
农用化肥施用折纯量(万吨) 0.9572 -0.2135
农业机械总动力(万千瓦) 0.8732 -0.4627
农村用电量(亿千瓦小时) 0.8593 -0.4665
成灾面积(千公顷) 0.5393 -0.7642
============================================================================
总方差解释表:
特征根 方差贡献率 累计方差贡献率
0 4.856384 0.911972 0.911972
1 0.468764 0.088028 1.000000
成分矩阵:
成分因子1 成分因子2
粮食作物播种面积(千公顷) 0.271971 0.728015
有效灌溉面积(千公顷) 0.740277 0.635653
农用化肥施用折纯量(万吨) 0.957188 0.213455
农业机械总动力(万千瓦) 0.873181 0.462703
农村用电量(亿千瓦小时) 0.859318 0.466468
成灾面积(千公顷) 0.539299 0.764158
因子得分:
成分因子1 成分因子2
年份
1991 -2.130235 -0.484807
1992 -2.036857 -0.474613
1993 -1.884693 -0.408794
1994 -1.409486 0.409563
1995 -1.413466 0.027594
1996 -1.270180 0.008348
1997 -0.823028 0.715448
1998 -0.889595 0.322387
1999 -0.761471 0.399934
2000 -0.361820 1.084371
2001 -0.255284 1.085971
2002 -0.211697 0.938587
2003 0.192310 1.626251
2004 -0.076590 0.602094
2005 0.171361 0.823237
2006 0.518959 1.221930
2007 0.749293 1.323718
2008 0.776516 0.990297
2009 0.913026 0.895940
2010 1.016440 0.696025
2011 0.989204 0.218415
2012 1.118643 0.148867
2013 1.292133 0.232977
2014 1.329402 0.020405
2015 1.325569 -0.194244
2016 1.096053 -0.279084
2017 0.879962 -0.781998
2018 0.740682 -0.954429
2019 0.466021 -1.467392
2020 0.124589 -1.664640
2021 -0.007105 -2.078383
2022 -0.062562 -2.388410
2023 -0.106095 -2.615565
综合得分:
粮食产量(万吨) 成分因子1 成分因子2 综合得分
年份
1991 43529.30 -2.130235 -0.484807 -1.985391
1992 44265.80 -2.036857 -0.474613 -1.899335
1993 45648.80 -1.884693 -0.408794 -1.754772
1994 44510.10 -1.409486 0.409563 -1.249358
1995 46661.80 -1.413466 0.027594 -1.286612
1996 50453.50 -1.270180 0.008348 -1.157633
1997 49417.10 -0.823028 0.715448 -0.687598
1998 51229.53 -0.889595 0.322387 -0.782906
1999 50838.58 -0.761471 0.399934 -0.659235
2000 46217.52 -0.361820 1.084371 -0.234514
2001 45263.67 -0.255284 1.085971 -0.137215
2002 45705.75 -0.211697 0.938587 -0.110440
2003 43069.53 0.192310 1.626251 0.318537
2004 46946.95 -0.076590 0.602094 -0.016846
2005 48402.19 0.171361 0.823237 0.228745
2006 49804.23 0.518959 1.221930 0.580840
2007 50413.85 0.749293 1.323718 0.799859
2008 53434.29 0.776516 0.990297 0.795335
2009 53940.86 0.913026 0.895940 0.911522
2010 55911.31 1.016440 0.696025 0.988235
2011 58849.33 0.989204 0.218415 0.921353
2012 61222.62 1.118643 0.148867 1.033275
2013 63048.20 1.292133 0.232977 1.198897
2014 63964.83 1.329402 0.020405 1.214173
2015 66060.27 1.325569 -0.194244 1.191782
2016 66043.51 1.096053 -0.279084 0.975002
2017 66160.73 0.879962 -0.781998 0.733662
2018 65789.22 0.740682 -0.954429 0.591465
2019 66384.34 0.466021 -1.467392 0.295826
2020 66949.15 0.124589 -1.664640 -0.032914
2021 68284.75 -0.007105 -2.078383 -0.189436
2022 68652.77 -0.062562 -2.388410 -0.267302
2023 69540.99 -0.106095 -2.615565 -0.326999